수학에 푸앵카레 추측 (Poincaré conjecture)라는 것이 있다.
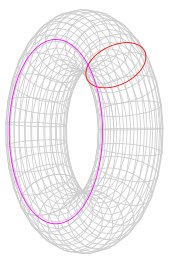
푸앵카레 추측 (Poincaré conjecture)은 4차원 초구의 경계인 3차원 구면의 위상학적 특징에 관한 다음과 같은 정리이다.
모든 경계가 없는 단일 연결 콤팩트 3차원 다양체는 3차원 구면과 위상동형이다.
(the Poincaré conjecture is a theorem about the characterization of the 3-sphere,
which is the hypersphere that bounds the unit ball in four-dimensional space.
The conjecture states: Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.)
이 명제는 프랑스의 저명한 수학자 앙리 푸앵카레의 1904년 논문에 처음 등장하는 추측으로,
우주의 형태에 대한 추측과도 밀접한 관련이 있다.
이 추측이 제기된 이래로 100여 년이 지난 후, 2002년, 2003년에 러시아의 저명한 수학자
그리고리 페렐만이 발표한 출간되지 않은 논문들에서 증명되었다. 밀레니엄 문제 중 최초로 해결되었다.
그는 2006년 필즈상 수상자로 선정하였으나, 페렐만은 수상을 거부하였다.
같은 업적으로 페렐만은 2010년 3월 18일 밀레니엄상의 수상자로도 선정되었으나, 밀레니엄상 역시 거부하였다.
그는 100만 달러를 거부하고 현재 상트페테르부르크의 한 아파트에서 어머니와 동거하며,
어머니의 연금을 통해서 어려운 생활을 하고 있는 것으로 알려져 있다.
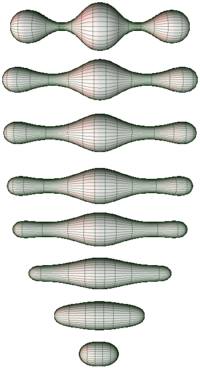
페렐만은 기하화 추측을 리처드 스트라이트 해밀턴이 발표한 리치 흐름(Ricci flow)을 사용해서 증명하였다.
리치 흐름은 3차원 리만 다양체를 더 대칭적으로 만드는 변환인데, 이 경우 유한한 시간 뒤에 다양체에 특이점이 발생하게 된다.
페렐만은 이러한 특이점의 성질과 구조를 분석하는 새로운 이론을 발표하였고, 이 기법을 사용해서 기하화 추측의 증명을 완성하였다.
아무튼 우리 수학자 모두는 약간씩 미친 거다.
(나같으면 그 100만 달러 받고 어머니를 더 행복하게 해드렸을 것 같다)